本篇文章给大家谈谈行列式的计算方法，以及3x3行列式计算示意图对应的知识点，文章可能有点长，但是希望大家可以阅读完，增长自己的知识，最重要的是希望对各位有所帮助，可以解决了您的问题，不要忘了收藏本站喔。

求行列式的值的方法总结

求行列式的值的方法总结如下：定义法：根据行列式的定义，通过逐行（或逐列）展开计算，得到行列式的值。这种方法对于较小的方阵较为适用，但对于大规模的方阵来说，计算量可能会非常大。公式法：利用行列式的展开公式，根据方阵的元素进行计算。

高斯消元法：这是求行列式值的一种常用方法。将一个 n 阶行列式转化为一个 n 阶方阵的行列式，然后通过高斯消元法求解该方阵的行列式。具体步骤如下：『1』 将行列式中的每一个元素都看作是一个未知数，构造一个 n 阶方程组。『2』 使用高斯消元法求解这个方程组，得到方程组的解。

行列式的计算方法主要依赖于其基本性质，以下是对行列式计算方法的总结：利用行列式的基本性质进行化简：对某行乘以常数k：行列式的值会变为k乘以原行列式。行列式行互换：会使行列式取相反数。一行的倍数加到另一行：行列式的值保持不变。

以第一行全为1的行列式为例。根据性质按第一行展开得D=1×A11+1×A12+...+1×A1n=A11+A12+..+A1n。第一行元素与其它行的代数余子式乘积之和为0，即k1时，0=1×Ak1+1×Ak2+...+1×Akn=Ak1+Ak2+..+Akn。

行列式的计算方法主要包括以下几种： 三角化方法：通过行列式的性质，将行列式转化为上三角或下三角形式，然后计算其对角线上的元素乘积得到结果。这种方法适用于可以直接或间接转化为三角形式的行列式。 展开法：利用行列式的性质，按照某一行或某一列展开，得到新的行列式进行计算。

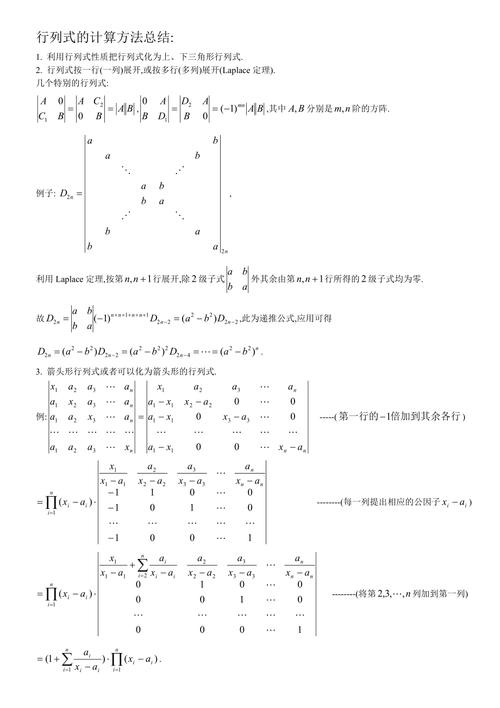
行列式相乘的计算方法是什么?

行列式相乘的计算方法如下：两个行列式相乘，首先必须是同阶方阵，其次，这两个方阵的行数和列数都必须是相同的。相乘时，将第一个方阵的行向量乘以第二个方阵的列向量，得到的结果是一个一阶行列式，再求这个一阶行列式的值，就得到了相乘的结果。

两个行列式相乘，先将前面矩阵的每一行分别与后面矩阵的列相乘作为结果矩阵的行列。当矩阵A的列数等于矩阵B的行数时，A与B可以相乘。矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

行列式的乘法公式其实是矩阵的乘法得来的，即|A||B|=|AB|；其中A.B为同阶方阵，若记A=（aij），B等于（bij），则|A||B|=|（cij）|，cij=ai1b1j+ai2b2j+...+ainbnj。行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det（A）或|A|。

行列式相乘的计算方法如下：确保两个矩阵的维度是兼容的。也就是说，第一个矩阵的列数必须等于第二个矩阵的行数。假设第一个矩阵是A，维度是m×n，第二个矩阵是B，维度是n×p，那么n必须相等。创建一个新的结果矩阵C，它的维度是m×p。

两个行列式相乘方法如下：两个行列式相乘，先将前面矩阵的每一行分别与后面矩阵的列相乘作为结果矩阵的行列。 当矩阵A的列数等于矩阵B的行数时，A与B可以相乘。 矩阵C的行数等于矩阵A的行数，C的列数等于B的列数。

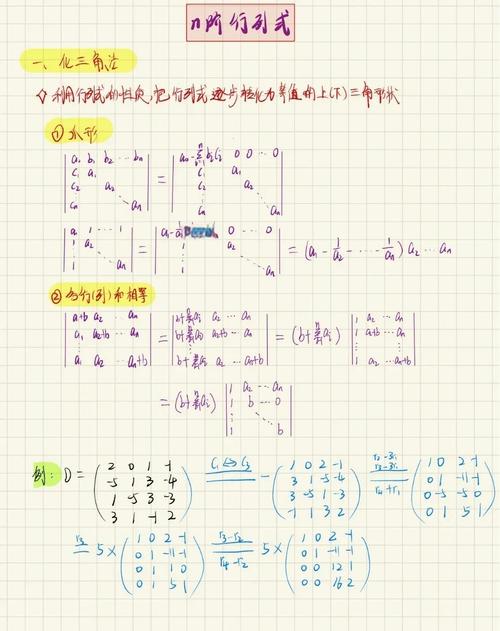
三阶行列式怎么算?

三阶行列式的计算方法如下：三阶行列式{（A，B，C），（D，E，F），（G，H，I）}，A、B、C、D、E、F、G、H、I都是数字。

一共有两种方法。对角线法：标准方法是在已给行列式的右边添加已给行列式的第一列、第二列。我们把行列式的左上角到右下角的对角线称为主对角线，把右上角到左下角的对角线称为次对角线。

三阶行列式可用对角线法则：D = a11a22a33 + a12a23a31 + a13a21a32- a13a22a31 - a12a21a33 - a11a23a32。

行列式怎么计算的?

利用行列式定义直接计算：行列式是由排成n阶方阵形式的n个数aij（i，j=1，2，...，n）确定的一个数，其值为n！项之和。利用行列式的性质计算：化为三角形行列式计算：若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。

行列式的乘法公式其实是矩阵的乘法得来的，即 |A||B| = |AB|；其中 A.B 为同阶方阵，若记 A=（aij），B=（bij），则|A||B| = |（cij）|，cij = ai1b1j+ai2b2j+...+ainbnj。行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det（A）或 | A | 。

单纯的一行三列的“行列式“已经不算是行列式，它的值没法计算，此时它应该是一个向量，几个向量之间的运算应按照向量的运算法则进行。

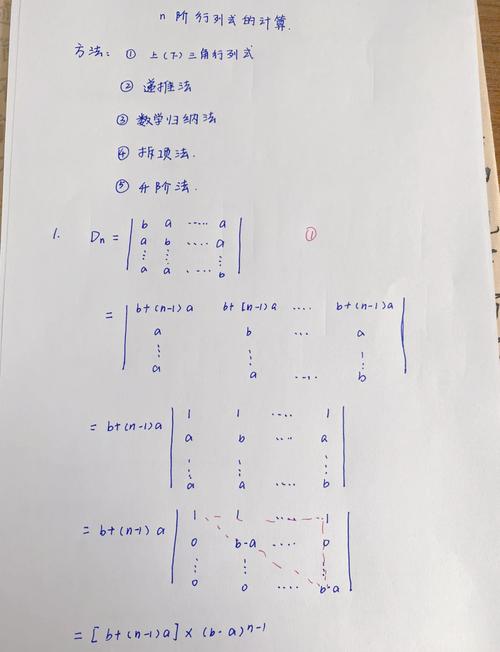
行列式是如何计算的?

〖壹〗、利用行列式定义直接计算：行列式是由排成n阶方阵形式的n个数aij（i，j=1，2，...，n）确定的一个数，其值为n！项之和。利用行列式的性质计算：化为三角形行列式计算：若能把一个行列式经过适当变换化为三角形，其结果为行列式主对角线上元素的乘积。因此化三角形是行列式计算中的一个重要方法。

〖贰〗、三阶行列式的计算方法如下：三阶行列式{（A，B，C），（D，E，F），（G，H，I）}，A、B、C、D、E、F、G、H、I都是数字。

〖叁〗、单纯的一行三列的“行列式“已经不算是行列式，它的值没法计算，此时它应该是一个向量，几个向量之间的运算应按照向量的运算法则进行。

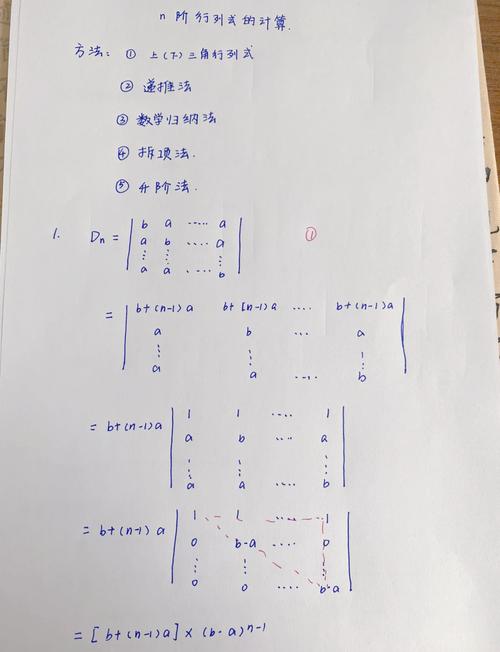
行列式有哪几种运算法则?

〖壹〗、行列式和它的转置行列式相等。行列式中某一行元素的公因子可以提到行列式符号的外边来，或者说，用一个数来乘行列式，可以把这个数乘到行列式的某一行上。若果行列式中有一行元素全为零，则行列式的值为零。交换行列式两行，行列式仅改变符号。

〖贰〗、行列式加减运算法则是只有一行（列）相加（减），其他行（列）不改变，与矩阵不同。行列式在数学中，是一个函数，其定义域为det的矩阵A，取值为一个标量，写作det（A）或|A|。无论是在线性代数、多项式理论，还是在微积分学中（比如说换元积分法中），行列式作为基本的数学工具，都有着重要的应用。

〖叁〗、行列式运算法则共有十条，包括三角的值、交换行列式、行列式展开、求解代数余子式、克拉默法则、齐次线性方程组等。具体内容如下：三角形行列式的值，等于对角线元素的乘积。计算时，一般需要多次运算来把行列式转换为上三角型或下三角型。交换行列式中的两行（列），行列式变号。

〖肆〗、行列式的运算性质主要包括以下几点：行列互换不变性：性质：行列式行列互换，其值不变。互换两行变号性：性质：互换行列式的两行，行列式的值会变号。公因子提取性：性质：如果行列式的某行有公因子，那么可以将这个公因子提出到行列式外面，行列式的值不变。

〖伍〗、行列式是线性代数中的一种重要工具，用于解决线性方程组、矩阵求逆、行列式的秩等问题。行列式的计算方法有多种，以下是其中几种常用的方法： 拉普拉斯展开法：将行列式按照某一行或某一列展开成多个小行列式的和。对于每个小行列式，可以递归地继续展开，直到得到一个1阶行列式，即一个数。

关于行列式的计算方法和3x3行列式计算示意图的介绍到此就结束了，不知道你从中找到你需要的信息了吗 ？如果你还想了解更多这方面的信息，记得收藏关注本站。